[翻译]功率电子基础 8.1

Fundamentals of Power Electronics

波特图

波特图是传递函数或者其他复数的幅频特性曲线，幅度使用分贝db作为单位，相位使用角度，使用对数轴。

幅度的无方向增益G可以表示为：

\[\left \| G \right \|_{dB}=20\log_{10}(\left \| G \right \|)\]

table.8.1

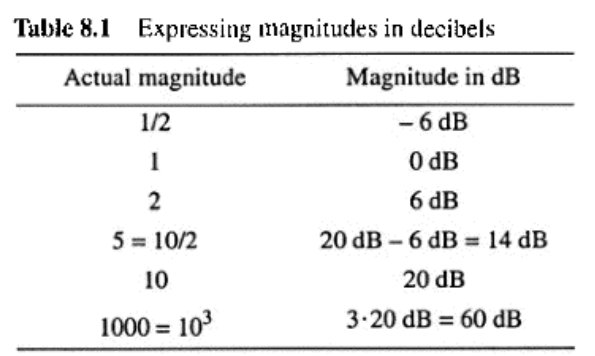
一些简单幅度的分贝值如Table 8.1.所示，需要注意当增益是有方向的时候。由于数的对数值没有方向的概念，幅度需要先进行归一化处理。例如，以db表示阻抗Z的幅度值，我们需要对阻抗Z除以一个基数Rbase得到归一化的数值。

\[\left \| Z \right \|_{dB}=20\log_{10}(\frac{\left \| Z \right \|}{R_{base}})\]

Rbase的可以是任意值，但我们需要告知他人所使用的值。所以如果|Z|是5欧，Rbase为10欧，可以得到 |Z|db = 20log10(5/10) = -6db （对于10欧来说）。通常Rbase可以选择为1欧，这样得到的单位就是db欧。因此5欧等同于14db欧。转换器输入电流谐波一般表示为dBuA，即归一化为1uA的dB值。60dBuA等同于1000uA，或者1mA。

幅度的波特图可以推导出f的能量是线性的。比如无方向量纲G(f)的幅度可以表示为

\[\left \| G \right \|=(\frac{f}{f_0})^n\]

式中f0和n都是常数，表示为dB值可以得到

\[\left \| G \right \|_{dB}=20\log_{10}(\frac{f}{f_0})^n=20n log_{10}(\frac{f}{f_0})\]

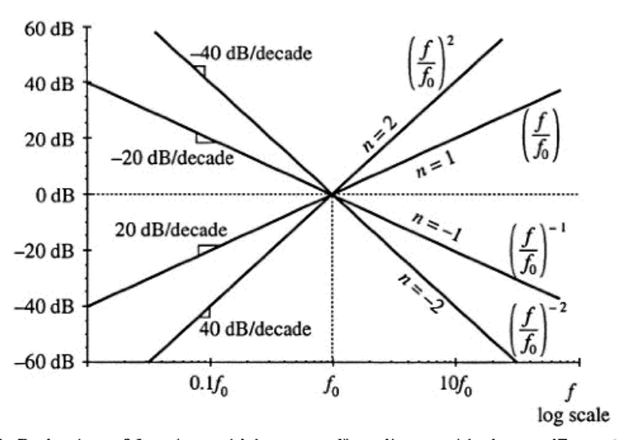
该等式对以不同n值可以参见Fig. 8.3。幅度在频率f=f0的时候可以得到幅度值1=>0dB。它们是log10(f)的线性方程。斜率表示对于log10(f)的一单位变化|G|dB的变化幅度，log10(f)的一单位变化表示频率f的10倍频变化。从8.6式可以看出，频率f的十倍频变化引起幅度|G|dB变化为20n dB。因此，斜率就是20n/十倍频。同样的，我们可以说斜率是20n log10(2) = 6n dB每八倍频，这里的八倍频表示频率的2的乘积变化。实际上，大部分频率相关的函数可以用一定范围的频率方程表示，方程的一般形式参见8.5式，在这些频率范围上，波特图可以近似为20n dB每十倍频变化。

fig.8.3

一个简单的单极点传递函数：

\[G(s)=\frac{1}{\frac{s}{w_0}}\]

幅度可以表示为

\[\left \| G(jw) \right \|=\frac{1}{\left \| \frac{jw}{w_0} \right \|}=\frac{1}{\frac{w}{w_0}}\]

我们定义f=w/2pi，则f0=w0/2pi，式8.8变化为

\[\left \| G \right \|=(\frac{f}{f_0})^{-1}\]

该式即为当n=-1的8.5式，如Fig. 8.3所示，8.7的波特图斜率为-20dB每十倍频，同时，在f=f0的时候通过0dB。

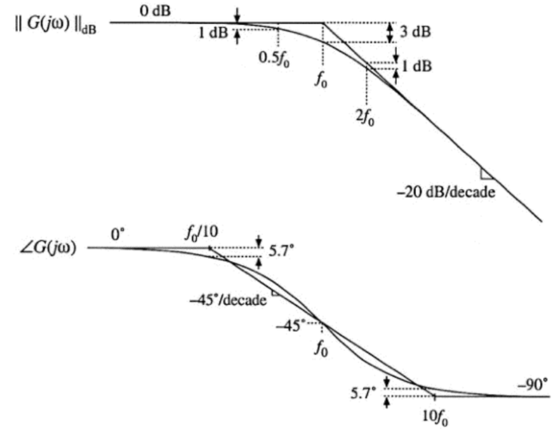
单极点响应

单极点传递函数的标准形式：

\[G(s)=\frac{1}{1+\frac{1}{w_0}}\]

［注］波特图一般估算过程：

fig.8.11

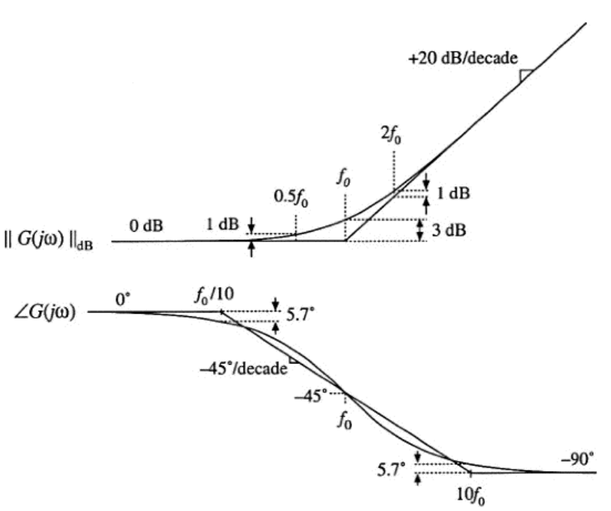
单零点响应

单零点传递函数的标准形式：

\[G(s)=1+\frac{s}{w_0}\]

波特图

fig.8.12

右半平面零点

标准形式

\[G(s)=1-\frac{s}{w_0}\]

波特图

fig.8.13

频率反转

反极点标准形式

\[G(s)=\frac{1}{1+\frac{w_0}{s}}\]

波特图

fig.8.14

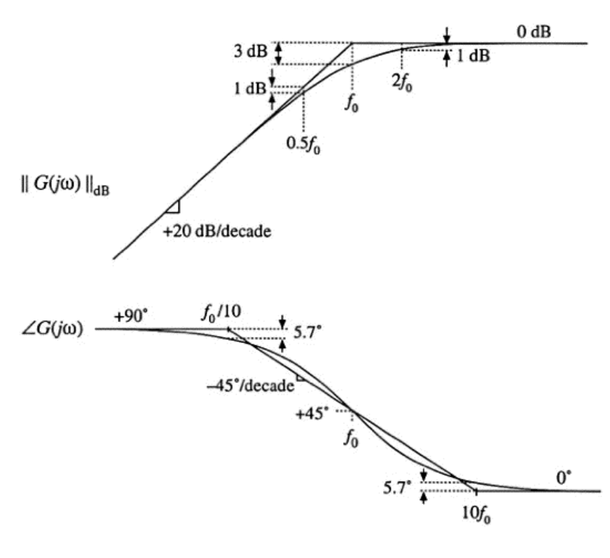
反零点标准形式

\[G(s)=1+\frac{w_0}{s}\]

波特图

fig.8.15

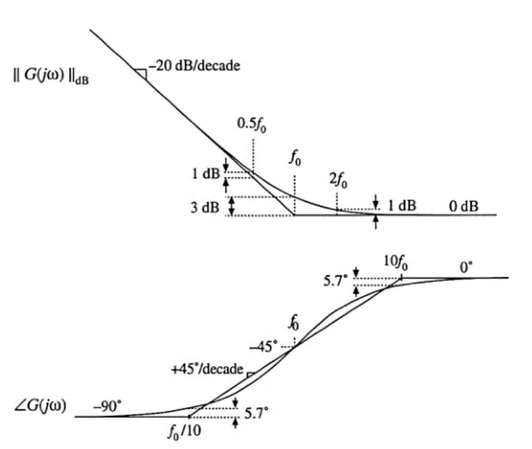
组合响应

举例来说，考虑一下传递函数的波特图：

\[G(s)=\frac{G_0}{(1+\frac{s}{w_1})(1+\frac{s}{w_2})}\]

G0=40(32dB), f1=w1/2pi=100Hz, f2=w2/2pi=2kHz

该传递函数包含3项：增益G0和在频率f1, f2的极点，渐近线如图8.16所示

fig.8.16

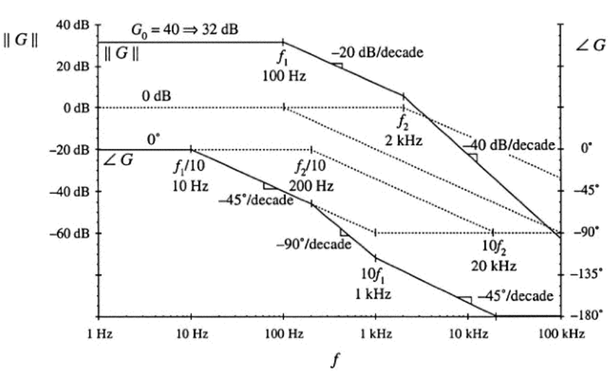
增益G0是正实数，在0频率贡献增益32dB，在100Hz和2kHz的极点对应的渐进线可以参考图8.11所示。

在小于100Hz的频率段，增益G0提供32dB的幅度增量，同时，两个极点提供趋近于0dB的幅度分量，因此低频幅度响应趋近于32dB+0dB+0dB=32dB。

在100Hz到2kHz的频率段，增益G0依然提供32dB的幅度分量，2kHz频率位置的极点也依然提供0dB的频率分量，但100Hz频率位置的极点的幅度渐进线是-20dB每十倍频。幅度响应曲线也因此以-20dB每十倍频斜率变化，如图8.16所示。

在大于2kHz的频率段，100Hz频率和2kHz频率位置到极点分别提供-20dB每十倍频斜率变化的分量，因此传递函数总计-20dB/decade + -20dB/decade = -40dB/decade。

相位变化渐进线在图8.16也有体现，小于10Hz的时候，所有分量贡献总和为0。在f1/10 = 10Hz 和 f2/10 = 200Hz 之间到频率段，主要由f1频率位置到极点提供-45/decade 的变化。在200Hz和10f1=1kHz之间到频率段，两个极点都提供-45/decade的分量，因此总计-90/decade。在1kHz和10f2=20kHz之间的频率段，频率f1位置到极点提供-90度的相位分量，而频率f2位置的极点提供-45/decade的频率变化，因而总计-45/decade。在大于20kHz的频率段，两个极点都提供固定相位分量-90度，总计-180度。

双极点响应